Selected poetry. 1 March 2010; 22:24
VAIN ATTEMPTS; PEACE FALSE
None brightens, though all shine
Riddle of the gap
Your silence, oh so divine
All gone.. no map
Fury is the silent killer
Coming to you when you sleep
Kindness, the dirge of hypocrisy
Only causing the masses to weep
Your ways are changed, yet they are not
Secular negation, contradiction complete
Yet coincidence, but a shadow of an illusion
All wolves ultimately compete
Are you a wolf?
.
"The surest way to corrupt a youth is to instruct him to hold in higher esteem those who think alike than those who think differently." - Friedrich Nietzsche
Saturday, November 24, 2012
SARTAJ: "BLUE"
Selected poetry. 5 March 2010; 22:45
BLUE
Blue renegade
Ejected energy
Waste of time
Down the drain
No more fight
I say to you..
Good night.
BLUE
Blue renegade
Ejected energy
Waste of time
Down the drain
No more fight
I say to you..
Good night.
Thursday, November 22, 2012
SARTAJ: A LOOK AT THE SPECIES PROBLEM
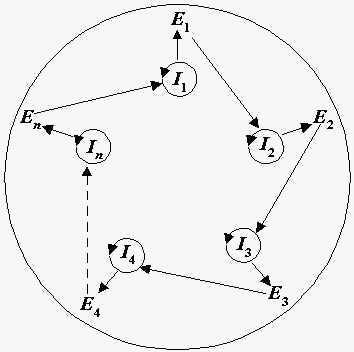
If it is unclear what is meant by closure, it is defined clearly by this example. Consider two elements or objects and assign one the symbol "*" and the other the symbol "~". When there is an interaction between * and ~, we call it a walk. When there is a walk from * to ~ and a walk from ~ to *, the set is called closed. Closed sets like these have been called auto-catalytic and have been implicated as being sources of order for the origin of life, with RNA as a classical example of such a closed system.
---
There can be no doubt that the term species denotes a set composed of organisms which can interbreed with one another, thus perpetuating an evolving spatiotemporal principle to a new generation, of which is composed a new set of unique individuals, operating and maintaining novel processes in their life-history. Largely, this firmness of belief stems from the operational usages of the term “species” in evolutionary biology. The existence of algorithms, such as hierarchical clustering, which can split populations of individuals into taxa, implies a real, although abstract, way of distinguishing finite attributes across a list of objects. Generally, hierarchical clustering, also called numerical taxonomy, is the process of producing groups of objects which share statistically meaningful pair-wise relationships among a list of chosen attributes for each object (2). The taxa that are generated by such a process can be as multi-dimensional as one would like, although the clustering of individuals into apparent classes should occur regardless of the system you are focusing on. As an example, clustering by genes would produce the same splitting as a clustering by phenotypic characteristics such as “wing length” and “head circumference” as measured in a group of some birds, although an observer could actually take both systems (the genetic and phenotypic) into account as variables assigned to their objects of study. I reject the notion that the entire set of such individuals is actually a natural kind in the sense that gold is a natural kind, as this multi-dimensional space in biological life is constantly evolving through time. Indeed, if one were to collect information about individual objects composing the class of all objects falling under “gold”, you may find over time that such a list of characteristics are also changing. The difference, perhaps, is that the method of clustering you choose to classify objects such as gold versus biological life produces a significant difference in variance. The change over thousands versus millions of years in gold apparently does not exhibit the novelty that biological life does at those time-scales.
Certainly, when you recognize that this method of clustering can take into consideration many levels of resolution, it must be recognized that the splitting of a feature-space into taxa will occur at many levels of resolution as well. Where do we distinguish applying the word species merely to a study involving the clustering of cells within an individual into groups as opposed to comparing actual biological individuals against one another? Once again, I would pretend to claim that this becomes operational matter. If it is experimentally useful to analyze the internal machinations of an individual and then assign observable clusters produced by them the name of “species”, then the observer is certainly entitled to do so. However, this must be distinguished from the act of how we consider a species in the domain of evolutionary biology; without that distinction, we would have no basis for considering when Homo sapiens diverged from its ancestral forms. Indeed, this notion we recognize as speciation is a benchmark of evolutionary theory. The other alternative is unifying these multiple resolutions by doing the following. If a biological individual is composed of cells, and natural selection posits that the fittest forms of life pass their spatiotemporal principle to a new generation, then the taxa of cells which continue to proliferate from a cluster x are the fittest for that individual. This cluster will continue to proliferate until such a time when the individual dies. Down to the resolution of the individual cell, the makeup that composes that cell from its original point of origin for the ontogeny of that organism from birth also uniquely proliferates insofar as being the informational element that initiates and survived from the moment of conception. Applying natural selection to the scale of unique components such as nucleic acids and proteins should also show us that only the fittest of them will continue to grow, whereas ones which contribute to those processes running counter to self-renewal would be discarded. We can continue an analysis in this fashion at all scales of resolution and organize the top clusters which have survived into the present into the nodes of what is called Eigen’s hypercycle (1). Such a hypercycle is organizationally closed, which means that all components are involved in a self-renewing process working towards maintaining the existence of the individual. The interaction also creates a closure between the individuals of the set called “species” which they are involved in, and this interaction is the ability of interbreeding at the level of resolution for a group of organisms. The hypercycle which survives is that closure between individuals in a set that manage to exist in the future, as well. In evolutionary time, once an observer in the future can note sufficient variance between these unique cycles at time-point X1 and X2, she may also recognize enough noticeable differences, whether from genetic analysis or the fossil record, that speciation has occurred. This type of analysis and recognition of apparently unique classes is something uncharacteristic of a natural kind and rejects the notion of an essential force underlying individuals or groups of them. Another particularly beautiful result of such a method also places the species problem as an ontological one. In the world of biology, ontological solutions in the questions of life have certainly allowed the scientists to at least deal with the deluge of data and biological information generated in the laboratory.
REFERENCES
1. Eigen, M., and P. Schuster. 1978. “Part A: Emergence of the Hypercycle.” Naturwissenschaften 65:7–41.
2. Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Section 16.4. Hierarchical Clustering by Phylogenetic Trees". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press.
There can be no doubt that the term species denotes a set composed of organisms which can interbreed with one another, thus perpetuating an evolving spatiotemporal principle to a new generation, of which is composed a new set of unique individuals, operating and maintaining novel processes in their life-history. Largely, this firmness of belief stems from the operational usages of the term “species” in evolutionary biology. The existence of algorithms, such as hierarchical clustering, which can split populations of individuals into taxa, implies a real, although abstract, way of distinguishing finite attributes across a list of objects. Generally, hierarchical clustering, also called numerical taxonomy, is the process of producing groups of objects which share statistically meaningful pair-wise relationships among a list of chosen attributes for each object (2). The taxa that are generated by such a process can be as multi-dimensional as one would like, although the clustering of individuals into apparent classes should occur regardless of the system you are focusing on. As an example, clustering by genes would produce the same splitting as a clustering by phenotypic characteristics such as “wing length” and “head circumference” as measured in a group of some birds, although an observer could actually take both systems (the genetic and phenotypic) into account as variables assigned to their objects of study. I reject the notion that the entire set of such individuals is actually a natural kind in the sense that gold is a natural kind, as this multi-dimensional space in biological life is constantly evolving through time. Indeed, if one were to collect information about individual objects composing the class of all objects falling under “gold”, you may find over time that such a list of characteristics are also changing. The difference, perhaps, is that the method of clustering you choose to classify objects such as gold versus biological life produces a significant difference in variance. The change over thousands versus millions of years in gold apparently does not exhibit the novelty that biological life does at those time-scales.
Certainly, when you recognize that this method of clustering can take into consideration many levels of resolution, it must be recognized that the splitting of a feature-space into taxa will occur at many levels of resolution as well. Where do we distinguish applying the word species merely to a study involving the clustering of cells within an individual into groups as opposed to comparing actual biological individuals against one another? Once again, I would pretend to claim that this becomes operational matter. If it is experimentally useful to analyze the internal machinations of an individual and then assign observable clusters produced by them the name of “species”, then the observer is certainly entitled to do so. However, this must be distinguished from the act of how we consider a species in the domain of evolutionary biology; without that distinction, we would have no basis for considering when Homo sapiens diverged from its ancestral forms. Indeed, this notion we recognize as speciation is a benchmark of evolutionary theory. The other alternative is unifying these multiple resolutions by doing the following. If a biological individual is composed of cells, and natural selection posits that the fittest forms of life pass their spatiotemporal principle to a new generation, then the taxa of cells which continue to proliferate from a cluster x are the fittest for that individual. This cluster will continue to proliferate until such a time when the individual dies. Down to the resolution of the individual cell, the makeup that composes that cell from its original point of origin for the ontogeny of that organism from birth also uniquely proliferates insofar as being the informational element that initiates and survived from the moment of conception. Applying natural selection to the scale of unique components such as nucleic acids and proteins should also show us that only the fittest of them will continue to grow, whereas ones which contribute to those processes running counter to self-renewal would be discarded. We can continue an analysis in this fashion at all scales of resolution and organize the top clusters which have survived into the present into the nodes of what is called Eigen’s hypercycle (1). Such a hypercycle is organizationally closed, which means that all components are involved in a self-renewing process working towards maintaining the existence of the individual. The interaction also creates a closure between the individuals of the set called “species” which they are involved in, and this interaction is the ability of interbreeding at the level of resolution for a group of organisms. The hypercycle which survives is that closure between individuals in a set that manage to exist in the future, as well. In evolutionary time, once an observer in the future can note sufficient variance between these unique cycles at time-point X1 and X2, she may also recognize enough noticeable differences, whether from genetic analysis or the fossil record, that speciation has occurred. This type of analysis and recognition of apparently unique classes is something uncharacteristic of a natural kind and rejects the notion of an essential force underlying individuals or groups of them. Another particularly beautiful result of such a method also places the species problem as an ontological one. In the world of biology, ontological solutions in the questions of life have certainly allowed the scientists to at least deal with the deluge of data and biological information generated in the laboratory.
REFERENCES
1. Eigen, M., and P. Schuster. 1978. “Part A: Emergence of the Hypercycle.” Naturwissenschaften 65:7–41.
2. Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Section 16.4. Hierarchical Clustering by Phylogenetic Trees". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press.
Thursday, November 8, 2012
SARTAJ: INDIVIDUALITY AND ONTOGENESIS
There is a particularly profound claim that Hull makes concerning organisms, which is that genes control the ontogeny of an organism. Although it is largely uncontroversial that Mendelian genetics shows us that some spatiotemporal principle is passed down from the parental generation to its offspring, I will address the view that genes are actually the principle underlying the ontogeny of a developmental system. Ontogeny, otherwise called morphogenesis, seeks to address how a member of a species actually comes to acquire its shape. If genes are considered to be a set of a string of DNA, then the ontogeny of an organism is implied by the unfolding of that DNA into a functional unit (protein), which subsequently informs the components of that organism precisely how a system within it will develop. A classic example of these phenomena is presented in embryogenesis, where the compartmentalization of segments such as the mesoderm is correlated with the activation of a gene circuit or particular concert of genes which encodes for that portion of the embryo. Aside from whether or not correlation does imply causation, the developmental systems view, as posited by characters such as Griffiths (1), directly contradicts genes as the causal factor for ontogenesis. As Hull apparently points out, the “unrestricted generalization” (2) of the scientific law underlying that of the gene ought to be reducible to the domain of physics and chemistry.
However, if an organism is an individual and genes are substituent, individual parts constituting the whole, then it should be the case that if genes are a necessary condition for the unfolding of such an ontogenic program, that all members across the spectrum of a species should fall under the same characteristics and/or phenotype. We can compare this to an example of a cue ball breaking a group of billiard balls; the entailing laws underlying the mechanics of the cue ball making contact with the preliminary grouping ought to produce the precisely same result in each instance. Clearly, this is not the case – a Pool player will tell you that not two breaks are the same. When analyzing the situation of ontogenesis, we can also see that from the realm of cellular biology up to that of the whole, functioning organism that no two members are precisely the same, either. One need only to look at n-number of Homo sapiens to see there is an endless diversity in – say – the ideas we generate about the apparent external world around us.
To address this, I claim that genes are not autonomous entities. By this, I mean that they cannot be individuals simply for the reason that they rely on the existence of the cell membrane. When one says that genes are not autonomous is to say that the dynamics underlying the conception of a distinctly unique member of a species transcend the boundaries of a naïve unfolding of some program which gives rise to the living unity of the organism. Although I do not pretend to claim that genes as entities denoted by DNA are actually passed down from parents to offspring, to say that some set of physico-chemical equations imply some structure of an organism coming to be discounts an entirely counter-intuitive nature of genic evolution. Consider the case of a red blood cell. It is quite common knowledge that the red blood cell is un-nucleated, which means that DNA will not be present within that biological structure. As a result, neither will genes (I suppose that DNA encodes genes). However, what we do observe is that the factor giving rise to red blood cells is passed down (parents and their children both have blood). It seems that the genic selectionists have some explaining to do with respect to this type of gene-independent ontogenesis. Although considering genes as individuals may be categorically useful, it certainly does not give us a complete account of the strange phenomena such as that presented by the red blood cell.
REFERENCES
1. Griffiths, PE. Gray, RD. (1994). Developmental Systems Theory and Evolutionary Explanation. J Phil. 91(6): 277-304.
2. Hull, DL. (1978). A Matter of Individuality. Phil Sci. 45(3): 335-360.
Tuesday, November 6, 2012
SARTAJ: ANALYTIC PHILOSOPHY - PART I
A Primer on Formal Logic: Part I of 'Analytic Philosophy' REVISED: 22 January 2012, 19 FEBRUARY 2012 SARTAJ HUNDAL Keywords: Frege, Russell, Wittgenstein, Analytic, Logic
I begin this series with a primer on the essential rules of formal logic. These rules are presented in the form of what are called "truth tables", forumlated by Ludwig Wittgenstein in the 20th century. The notion of truth tables arguably originated with Frege, who first defined what it means for a statement to fall under what he called 'The True' and 'The False' ("Begriffsschrift", 1879) As this series unfolds, contributions made to the fields of formal logic and analytic philosophy by Frege and Russell will be included. If this blog can ever profess to be written by 'Philosophers with hammers', then indeed formal logic is the hammer with which our positions are tempered with.
A word of caution.. just because an argument is logical does not make it
reasonable. For example, consider:
(1) If the sun is square, then my cat has claws.
The above sentence (1) can be denoted in the material form:
(2) The sun is square => my cat has claws.
Where "=>" means 'implies' (see Material Implication table below). In this case, it is FALSE that the sun is square, but it is TRUE that a cat has claws. HOWEVER, by definition of the material implication, the entire statement is actually TRUE. It is clear that that (1) is actually completely unreasonable, but by the formal rules is logically sound. In this manner, it is important to understand first that formal logic is a tool to assist us in dissecting and formulating arguments. That said, the ART of formulating a reasonable and logically sound argument is up to the individual in their chosen mode of discourse.
Use these tools wisely.
Symbols:
^ = 'AND', Logical Conjunction
v = 'OR', Logical Disjunction
x = 'XOR', Exclusive Disjunction
~ = 'NOT', Negation, Logical Complement
T or 1 = TRUE
F or 0 = FALSE
In computer science speak, T is denoted as 1, and F is denoted as 0. The reasons for this are underlied by the binary (logarithm with a base of 2) logic circuits which innervate hardware/software interfaces, where any logical expression can be represented by a series of binary "logic gates".
Using these symbols, we can begin to analyze very simple to complex
statements.
Truth Tables (A and B are objects, sentences) Logical Conjunction A ^ B T T T T F F F T F
F F T Logical Disjunction A v B T T T T F T F T T F F F Exclusive Disjunction (AKA xor; the exclusive 'or') A X B T T F F F F T F T F T T Material Implication A => B T T T F T T (Vacuous truth) T F F F F F Biconditional Logical Connective (IFF, If and only if) A<=>B T T T T F F F T F F F T
Thursday, November 1, 2012
SARTAJ: TOWARDS THE PANTHEON OF INFINITY
My previous post introduced concepts such as contingency and attraction. With this small essay I seek to open up some brick roads to matters of time and evolution, although you should really take a look at the articles I reference if you want to see how the "masters" do it.
--
Written for Philosophy of Biology (PHIL565 at the University of Calgary)
Professor: Marc Ereshefsky <http://people.ucalgary.ca/~ereshefs/>
Let us begin with Reichenbach’s common-cause principle. The principle states that simultaneous correlated events must have prior common causes (1). Specifically, for events x and y, when the probability of x and y occurring together is greater than the probability of x and y occurring independently of each other, there exists a “common-cause” z where it is true that: Pr(x/z) > Pr(x/~z), Pr(y/z > Pr(y/~z), Pr(x&y/z) = Pr(x/z) × Pr(y/z) and Pr(x&y/~z) = Pr(x/~x) × Pr(y/~z), where the symbol “Pr” denotes the probability of an event. It is upon this principle that, as Cleland argues (3), narratives about the distant past are generated. I will demonstrate that such narratives generated by the principle are insufficient for explaining why the states of affairs of the present are the way they are.
Under a physics worldview we ought to be able to observe the world around us and write a story about the dynamics of that system. When this story has been written, observers use those tools to make claims about events in the past. For example, that volcanoes erupt today and have an underlying model to explain their behaviour lends weight to the fact that perhaps volcanoes occurred in the past as well and share similar behaviour. However, in the history of time, there are some problems with the notion of extending such a worldview to the past. First, an observer cannot know the entire phase-space of the system that they are studying – this is a particularly difficult when you attempt to travel back in time. Second, since the phase space of a system is not prestatable, the asymmetry of overdetermination is rendered useless since it is never guaranteed that an observer can derive the common-cause because some set of effects occur. Now, keeping this in mind, suppose that there are no entailing laws, but enablement, for the evolution of the biosphere (2). By enablement, I mean that in an historical network, life emerges out of a web where the changing conditions of space and time “lock into” a moment such that novelty may arise, although not necessarily. That the conditions for something to materialize exist does not guarantee it will actually happen. For example, if a hostage is taken and a hero has a villain in a clear line of sights down their rifle, the hero is not guaranteed to take the shot – evolution could work the same way. Under this pretext, as the biosphere bubbles forth, the laws which are created over time to account for observable phenomena exist at the level of the phase-space. In turn, this phase-space has and will continue to evolve as the staggering diversity of variables, forms and niches are enabled in the biosphere. Since the physical phase-space is ever-evolving, any method we devise to generate our historical narrative will become contingent upon the axioms derived from those observations (à la Gödel’s incompleteness theorem). What I am not trying to say is that the world is unobservable or that an entailing laws worldview is entirely useless, but that the layer at which we generate narratives is grounded in the symmetries of such an axiomatic method, where the predictive power of the mathematical form our narrative takes is not restrained within the confines of a material reality. A mathematical form in this context becomes an operational description based on symbols, but will not actually inform us about what the specific components of events in the past are. Since these components are unknowable as ultimate ends to the effects leading to the present state of affairs, any historical narrative created as a result of our observation is rendered a correlation as opposed to having any one explanation as an overdetermining cause (e.g.; meteor impact versus pandemic in the extinction of dinosaurs).
With respect to this notion of symmetry, Longo and Montévil assert that objects in the physical world continually transform and renew their symmetries (called symmetry change) (4) which give rise to the variance seen at all scales of existence, lending an ear to concepts such as fractal geometry. Mathematically, as symmetries change over time, the object passes over a continuous landscape and enters into and breaks critical points, which could actually give rise to processes such as biological evolution itself under some conditions-N when given enough time (tending towards infinity). In the context of historical narratives, the breaking of critical points over time represents instances where a set of objects observed in the present may allow us to observe how a state of affairs came to be today, but since the domain of discourse used to study that phenomena depends on the state variables of the present, we ought not have confidence that the entailing laws of today necessarily constrain the symmetry of that object in the past. When applied to the common-cause principle, a “screener” cause z is a selection of the one of many such objects. Choosing just one is not only inadequate, but it provides no account for the self-similarity seen through time in the patterns of organization implied by the renewal and projection of objects whose symmetries evolve at such critical points.
REFERENCES
1. Reichenbach, H. (1956). “The Direction of Time”, Berkeley, University of Los Angeles Press.
2. Longo, G., Montévil, M., Kauffman, SA. (2012). “No entailing laws, but enablement in the evolution of the biosphere”, Proceedings of the fourteenth international conference on Genetic and evolutionary computation conference companion (GECCO Companion '12), Terence Soule (Ed.). ACM, New York, NY, USA, 1379-1392. DOI=10.1145/2330784.2330946 http://doi.acm.org/10.1145/2330784.2330946
3. Cleland, CE. (2011). “Prediction and Explanation in Historical Natural Science”, Brit. J. Phil. Sci., 62: 551-582.
4. Longo, G., Montévil, M. (2012). “From physics to biology by extending criticality and symmetry breakings”, Prog. Biophys. Mol. Biol., 106(2): 340-347.
--
Written for Philosophy of Biology (PHIL565 at the University of Calgary)
Professor: Marc Ereshefsky <http://people.ucalgary.ca/~ereshefs/>
Let us begin with Reichenbach’s common-cause principle. The principle states that simultaneous correlated events must have prior common causes (1). Specifically, for events x and y, when the probability of x and y occurring together is greater than the probability of x and y occurring independently of each other, there exists a “common-cause” z where it is true that: Pr(x/z) > Pr(x/~z), Pr(y/z > Pr(y/~z), Pr(x&y/z) = Pr(x/z) × Pr(y/z) and Pr(x&y/~z) = Pr(x/~x) × Pr(y/~z), where the symbol “Pr” denotes the probability of an event. It is upon this principle that, as Cleland argues (3), narratives about the distant past are generated. I will demonstrate that such narratives generated by the principle are insufficient for explaining why the states of affairs of the present are the way they are.
Under a physics worldview we ought to be able to observe the world around us and write a story about the dynamics of that system. When this story has been written, observers use those tools to make claims about events in the past. For example, that volcanoes erupt today and have an underlying model to explain their behaviour lends weight to the fact that perhaps volcanoes occurred in the past as well and share similar behaviour. However, in the history of time, there are some problems with the notion of extending such a worldview to the past. First, an observer cannot know the entire phase-space of the system that they are studying – this is a particularly difficult when you attempt to travel back in time. Second, since the phase space of a system is not prestatable, the asymmetry of overdetermination is rendered useless since it is never guaranteed that an observer can derive the common-cause because some set of effects occur. Now, keeping this in mind, suppose that there are no entailing laws, but enablement, for the evolution of the biosphere (2). By enablement, I mean that in an historical network, life emerges out of a web where the changing conditions of space and time “lock into” a moment such that novelty may arise, although not necessarily. That the conditions for something to materialize exist does not guarantee it will actually happen. For example, if a hostage is taken and a hero has a villain in a clear line of sights down their rifle, the hero is not guaranteed to take the shot – evolution could work the same way. Under this pretext, as the biosphere bubbles forth, the laws which are created over time to account for observable phenomena exist at the level of the phase-space. In turn, this phase-space has and will continue to evolve as the staggering diversity of variables, forms and niches are enabled in the biosphere. Since the physical phase-space is ever-evolving, any method we devise to generate our historical narrative will become contingent upon the axioms derived from those observations (à la Gödel’s incompleteness theorem). What I am not trying to say is that the world is unobservable or that an entailing laws worldview is entirely useless, but that the layer at which we generate narratives is grounded in the symmetries of such an axiomatic method, where the predictive power of the mathematical form our narrative takes is not restrained within the confines of a material reality. A mathematical form in this context becomes an operational description based on symbols, but will not actually inform us about what the specific components of events in the past are. Since these components are unknowable as ultimate ends to the effects leading to the present state of affairs, any historical narrative created as a result of our observation is rendered a correlation as opposed to having any one explanation as an overdetermining cause (e.g.; meteor impact versus pandemic in the extinction of dinosaurs).
With respect to this notion of symmetry, Longo and Montévil assert that objects in the physical world continually transform and renew their symmetries (called symmetry change) (4) which give rise to the variance seen at all scales of existence, lending an ear to concepts such as fractal geometry. Mathematically, as symmetries change over time, the object passes over a continuous landscape and enters into and breaks critical points, which could actually give rise to processes such as biological evolution itself under some conditions-N when given enough time (tending towards infinity). In the context of historical narratives, the breaking of critical points over time represents instances where a set of objects observed in the present may allow us to observe how a state of affairs came to be today, but since the domain of discourse used to study that phenomena depends on the state variables of the present, we ought not have confidence that the entailing laws of today necessarily constrain the symmetry of that object in the past. When applied to the common-cause principle, a “screener” cause z is a selection of the one of many such objects. Choosing just one is not only inadequate, but it provides no account for the self-similarity seen through time in the patterns of organization implied by the renewal and projection of objects whose symmetries evolve at such critical points.
REFERENCES
1. Reichenbach, H. (1956). “The Direction of Time”, Berkeley, University of Los Angeles Press.
2. Longo, G., Montévil, M., Kauffman, SA. (2012). “No entailing laws, but enablement in the evolution of the biosphere”, Proceedings of the fourteenth international conference on Genetic and evolutionary computation conference companion (GECCO Companion '12), Terence Soule (Ed.). ACM, New York, NY, USA, 1379-1392. DOI=10.1145/2330784.2330946 http://doi.acm.org/10.1145/2330784.2330946
3. Cleland, CE. (2011). “Prediction and Explanation in Historical Natural Science”, Brit. J. Phil. Sci., 62: 551-582.
4. Longo, G., Montévil, M. (2012). “From physics to biology by extending criticality and symmetry breakings”, Prog. Biophys. Mol. Biol., 106(2): 340-347.
Subscribe to:
Posts (Atom)